The Binomial Distribution


-
Suppose that we have an experiment such as tossing a coin or a die repeatedly. Each toss or selection is called a trial. In any single trial there will be a probability associated with a particular event such as head on the coin or 4 on the die. This probability will not change from one trial to the next. Such trials are then said to be independent and are often called Bernoulli trials after James Bernoulli who investigated them at the end of the 17th century.
Let p be the probabiltiy that an event will happen in any single Bernoulli trial (the probability of success). Then q = 1 - p is the probability that the event will fail to happen in any single trial (the probability of failure). The probability that the event will happen exactly x times in n trials ( x successes and n - x failures will occur) is given by the probability function:
Binomial Distribution
 where:
where:
- p is the probability of success
- q (1-p) is the probability of failure
- n is the number of trials
- X (the random variable
) is the number of successes in n trials and x = 0, 1, ...., n.
-
Example:
-
What is the probability of getting exactly 2 heads in 6 tosses of a fair coin?
Solution:
P(X = 2) = 6! / (2! 4!) (1/2)2 (1/2)6-2 = 15/64
Are you wondering how to get the above solution?
Simply substitute the values of 2 and 6 in place of x and n respectively in the above equation, and get the required result.
The discrete probability function given in the above equation is often called the binomial distribution since for x = 0, 1, 2, ..., n it corresponds to successive terms in the binomial expansion.
Binomial Expansion
 where:
where:
- p is the probability of success
- q (1-p) is the probability of failure
- n is the number of trials
- X (the random variable
) is the number of successes in n trials and x = 0, 1, ...., n.
The above result is also called the Bernoulli distribution.
An example of Binomial distribution curve
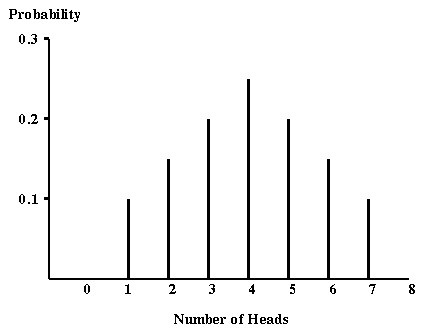
Properties of Binomial Distribution
| Mean | np |
| Variance | npq |
| Standard deviation | (npq)1/2 |



