Single Class Model

In this model of a system, all transactions in the system have the same requirements for use of the servers in the system. It is not necessary to consider each transaction, rather the total number of transactions in the system at one time is important. [M2] This example of a queueing network represents a single class model. The CPU processes transactions in the active set until a transaction receives a page fault. The transaction that receives the page fault moves to the page disk where its memory is reallocated. Then, it returns to the CPU to continue processing. When processing is complete, the transaction leaves the system. [D6]

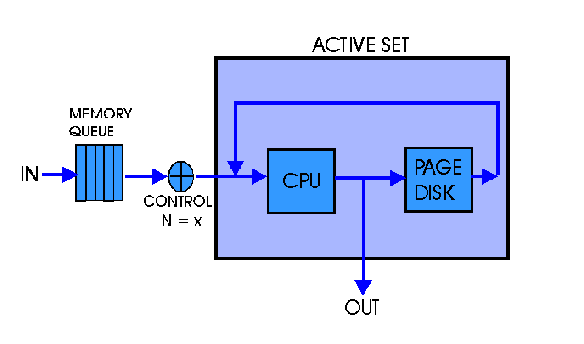
This example also represents a closed system. The control unit regulates the load (N) on the system allowing only x transactions to be serviced at a time. The system load in this example is the same as the degree of multiprogramming. If there is a maximum load on the system, transactions requiring service wait in the memory queue. The conrol unit allows a transaction from the queue to enter the system when a transaction leaves the system. This is one example of a simple system represented in a queueing network model. The queueing network model can be expanded to provide data on systems with significantly more servers or a system that services different types of transactions in different ways.

System throughput and response time are important measures of system performance. Using the queuing network model and a series of calculations, called mean value analysis the throughput and response time of a system can be determined. Other calculations can pinpoint the effect of a server's performance on the entire system. The calculations, derived from three operational laws, begin with the visit ratio and mean service time for each server. [D4] and [M2]