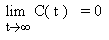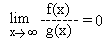What are the properties of limits?

Property # 1
Consider the problem in which one has to find the limit for a constant, say 3. The limit is written as:
 As it can be seen, there is no variable term in the function. The only term present is the constant 3. So the final result would be simply 3.
This property is briefly explained below :
As it can be seen, there is no variable term in the function. The only term present is the constant 3. So the final result would be simply 3.
This property is briefly explained below :
The limit of a constant is the constant itself. This can be expressed in the following form :
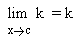 where k and c are constants.
where k and c are constants.

Property # 2
Consider the problem of finding the limit of a function f(x)= x2 - x + 1 when x tends to 2 :
 The procedure for finding the limit of the function as x tends to 2 is to substitute the value of x in the function and determine the value of the function.
The procedure for finding the limit of the function as x tends to 2 is to substitute the value of x in the function and determine the value of the function.
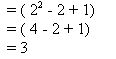
Now, consider the problem of finding the limit of a function f(x) which is a sum of two functions g1(x)= x3 - x2 + x + 1 and g2(x) = x2 - x + 1 when x tends to 2 :
We have
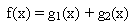
 The procedure for finding the limit of the function as x tends to 2 is to substitute the value of x in each function and determine the value of the function.
The procedure for finding the limit of the function as x tends to 2 is to substitute the value of x in each function and determine the value of the function.
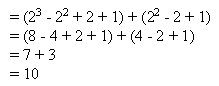 This property is briefly explained below :
This property is briefly explained below :
The limit of a sum (or difference) of the functions is the sum (or difference) of the limits of the individual functions. This can be expressed in the following form :
 if c is a constant and also if the limits of the two functions g1 and g2 are finite.
if c is a constant and also if the limits of the two functions g1 and g2 are finite. 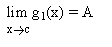
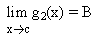 .
.

Property # 3
Consider the problem in which one has to find the limit for the following function :
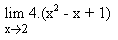 On observation you would find that the previous function is multiplied by 4. The value of the limit can be found out as demonstarted below :
On observation you would find that the previous function is multiplied by 4. The value of the limit can be found out as demonstarted below :
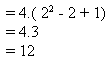 The value of the limit is a simple multiplication of the final value of the previous limit by 4.
This property is briefly explained below :
The value of the limit is a simple multiplication of the final value of the previous limit by 4.
This property is briefly explained below :
The limit of a function multiplied by a constant is equal to the value of the function multiplied by the constant which is expressed as follows :
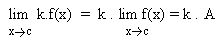
if the value of the function is A.i.e.,


Property # 4
Consider the problem in which one has to find the limit for the follow
ing function as x -> 3 :
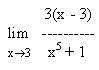 The value of the limit is found out by simply substituting the value of x in the function.
The value of the limit is found out by simply substituting the value of x in the function.
 This can be simply expressed in the following form :
This can be simply expressed in the following form :
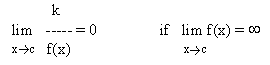

Property # 5
Consider the problem in which one has to find the limit for the following function :
 The value of the limit is found out by simply substituting the value of x in the function.
The value of the limit is found out by simply substituting the value of x in the function.
 This can be simply expressed in the following form :
This can be simply expressed in the following form :


Property # 6
Consider the function in the example given in the previous page. The graph has been plotted for the function C(t).
 We observe from the graph that the value of the function depends entirely on the denominator for large values of t. The denominator has t 2 term and the numerator has only t term. For large values of t, 3 in the denominator can be omitted. Thereby the function reduces to the following form
We observe from the graph that the value of the function depends entirely on the denominator for large values of t. The denominator has t 2 term and the numerator has only t term. For large values of t, 3 in the denominator can be omitted. Thereby the function reduces to the following form 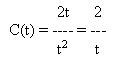 which is further reduced to 2/t. Thus, the value of the function depends entirely on the denominator.
It becomes 0 when t tends to
which is further reduced to 2/t. Thus, the value of the function depends entirely on the denominator.
It becomes 0 when t tends to  which is written as :
which is written as :
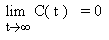
This property can be restated in the following simple form :
Consider two polynomials f(x) and g(x). Let f(x) be a polynomial of degree n and g(x) be a polynomial of degree m. Then, we can state, if m > n > 1, as follows:
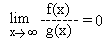


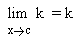

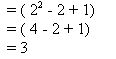
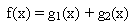

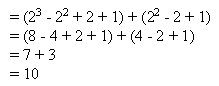

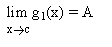
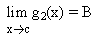
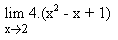
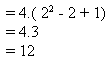
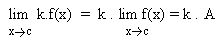

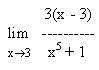

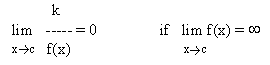




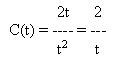
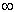 which is written as :
which is written as :