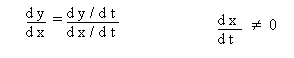Here are some basic laws which can be used to derive other differentiation rules.

 The derivative of a constant is zero.
The derivative of a constant is zero.

 The derivative of the product of a constant and a function is equal to the constant times the derivative of the function.
The derivative of the product of a constant and a function is equal to the constant times the derivative of the function.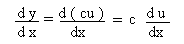

 The derivative of the sum or difference of two functions is equal to the sum or difference of the derivatives of the functions
The derivative of the sum or difference of two functions is equal to the sum or difference of the derivatives of the functions

 The derivative of the product of two functions is equal to the first function times the derivative of the second, plus the second function times the derivative of the first
The derivative of the product of two functions is equal to the first function times the derivative of the second, plus the second function times the derivative of the first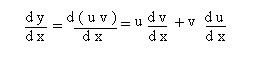

 The derivative of a fraction, that is, the quotient of two functions, is equal to the function in the denominator times the derivative of the function in the numerator, minus the function in the numerator times the derivative of the function in the denominator, all divided by the square of the function in the denominator
The derivative of a fraction, that is, the quotient of two functions, is equal to the function in the denominator times the derivative of the function in the numerator, minus the function in the numerator times the derivative of the function in the denominator, all divided by the square of the function in the denominator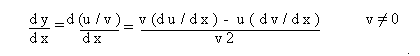

 If the derivative of y = f(x) is dy/dx, then the derivative of the inverse function which expresses x in terms of y is given by the formula
If the derivative of y = f(x) is dy/dx, then the derivative of the inverse function which expresses x in terms of y is given by the formula 

 If y = f(u) and u = g(x), that is, if y is a function of a function, then
If y = f(u) and u = g(x), that is, if y is a function of a function, then 

 If y = f(t) and x = g(t), that is, if y and x are related parametrically, then
If y = f(t) and x = g(t), that is, if y and x are related parametrically, then