


In the previous example, we had an equation of the form:
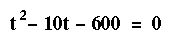
which we factored into two terms as follows:
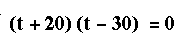
The answer would be t = -20 and t = 30. Since -20 has no meaning,
the answer is simply 30.
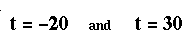

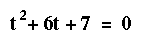


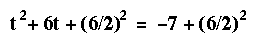
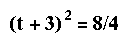
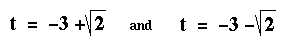



 Use factoring when the equation is simple and the factors are obvious. Use
completing the square when you cannot factor the equation.
When in doubt, use the Quadratic Formula, shown on the next page,
which works for any quadratic equations.
Use factoring when the equation is simple and the factors are obvious. Use
completing the square when you cannot factor the equation.
When in doubt, use the Quadratic Formula, shown on the next page,
which works for any quadratic equations.



 Homepage Subway map Exercises Quadratic Back Forward
beginning
Homepage Subway map Exercises Quadratic Back Forward
beginning