








Processes
Introduction
Races/Exclusive Use
Arbitration
Synchronization
Deadlocks
Time Sharing
Authors:
Halleh Fatheisian
Eric Rosenberger
Deadlocks
The methods discussed so far -- for arbitration, mutual exclusion, and synchronization -- are all "local" in that they deal with a particular interaction among particular processes. With an arbiter, we can safely choose one of two simultaneous events. With a mutual excluder, we can safely allow any process to perform an operation on a shared object without interference from another process. With a synchronizer, we can force one process to stop and wait for a signal from another.
But what about the larger picture? What about a system of many processes sharing many resources and exchanging many signals? Can anything go wrong in the system that cannot go wrong in the local interactions?
The answer is: indeed, yes! The single most important coordination problem to strike a system of processes is the deadlock, a condition in which a set of processes are all stopped and waiting for a signal from another member of the set.

|
Deadlocks occur in human systems with striking regularity. The traffic gridlock is the most common example. A simple gridlock occurs in an intersection when two lines of cars are attempting to turn left and the path of the front car is blocked by cars in the other line. A simple gridlock can turn into a regional gridlock if the lines of cars back up into other intersections. People in big-city areas know well how a snowstorm can cause a regional deadlock: nothing moves on any major artery.
A Kitchen Example
An example long used by computer systems designers to illustrate the problem
of deadlocks is inspired by the analogy between algorithms and recipes. This
example, which was first used around 1965 by Edsger Dijkstra, takes place in
a gourmet kitchen with one burner and one hand-mixer. The stew recipe calls
for the ingredients to be blended and then simmered on the burner; a few
minutes before it is done, the chef is to use the mixer smooth the stew, and
is to continue the mixing until a few minutes after removing the pot from the
burner. The pudding recipe calls for the ingredients to be combined; the chef
is then to use the mixer to blend them; while continuing to mix, place the
pot on the burner until the mixture reaches critical temperature; and to
remove from burner a few minutes later. If we try to automate this kitchen
using semaphores burner and mixer, both initialized to 1, we
obtain:
Stew: 1 combine ingredients; Pudding: 1 combine ingredients;
2 WAIT(burner); 2 WAIT(mixer);
3 cook; 3 mix;
4 WAIT(mixer); 4 WAIT(burner);
5 cook and mix; 5 cook and mix;
6 remove from burner; 6 stop mixing;
7 SIGNAL(burner); 7 SIGNAL(mixer);
8 mix a while longer; 8 cook a while longer;
9 SIGNAL(mixer); 9 SIGNAL(burner);
10 serve 10 serve
Let's use two numbers to represent the state of this kitchen: (x,y) means the stew is at step x and pudding at step y. The initial state is (0,0) and the final state is (10,10). The objective of the chef is to guide the recipes from initial to final state. Can this always be done?
Well, no. Suppose the kitchen comes to state (4,4). There we see the stew waiting for the mixer, which it cannot get because the pudding already has the mixer; and the pudding is waiting for the burner, which it cannot get because the stew already has the burner. Now the chef is really stuck! The only way out is to scrap one of the recipes and start it over again. There is no other way, because the chef cannot run the recipe backwards.
Obviously the chef must not allow the kitchen to enter state (4,4). But it is worse than this. If either process reaches its step 2, and the other is allowed to reach or pass step 2, the deadlock is unavoidable. It hasn't happened yet, but eventually it will. The states (2,2), (2,3), (2,4), (3,2), (3,3), (3,4), (4,2), and (4,3) are all unsafe because deadlock will eventually occur if the kitchen gets into any one of these states. This seriously complicates the chef's job because of the need to keep the kitchen in only safe states. In a busy kitchen with many more recipes in preparation and many more resources to draw on, this is likely to overtax the chef.
Prevention Strategies
Are there any strategies that the chef can use to prevent the kitchen from ever entering a deadlock state? One is to rearrange the recipes so that they acquire all resources they need before they begin. In this case, both the stew and pudding would request the burner and mixer before beginning; an arbiter would decide which request to honor if both arrived simultaneously. Then the possibility of deadlock is removed.
Another strategy is to assign a strict ordering to the resources and restrict processes from requesting any new resource of a lower priority than the highest already held. In this case, if mixer were lower priority and burner of higher, we would have to rearrange the stew recipe so that it acquires both the mixer and burner (in that order) before the remaining steps are undertaken.
| Both these strategies are aimed at invalidating the central condition of a deadlock: the circular wait. |
Both these strategies are aimed at invalidating the central condition of a deadlock: the circular wait. In the get-all-at-start strategy, there is only one wait point (at the beginning); it's not possible for any process to stop and wait again. In the priority strategy, there must always be a process that is holding its highest priority resource; hence it cannot wait and will eventually release what it does hold for others to use.
Avoidance Strategies
The prevention strategies are quite conservative. They restrict the acquisition of resources in ways that prevent a circular wait from occurring; but they waste resources in order to do this. The get-all-at-start strategy is likely to cause the process to hold some resources for a long time before it actually uses them; those resources are not available for others to use. The priority strategy makes it difficult to obtain a second instance of the same resource (e.g., a second burner) once you've got the first. Are there any strategies that place no restrictions on how often a process can come back and request more resources without allowing the system into an unsafe state?
There are, and we need to look at a different analogy to how they work. The
analogy of a banking system was first used around 1970 by Nico Habermann.
Habermann was a citizen of The Netherlands, which has a long and venerable
history of conducting mercantile transactions in multiple currencies. We can
illustrate the problem, however, with people borrowing money of a single
currency from a bank with limited reserves. Consider two customers, Alice and
Bob. Both have applied for and received lines of credit: Alice's credit limit
is $10 and Bob's $20. Either can approach the bank at any time to borrow
additional funds (up to their personal credit limits) or to repay some or all
of their outstanding loans. Here is an example of their borrowing and
repayment patterns:
Alice: plan; Bob: plan;
borrow(8); borrow(16);
various actions; various actions;
borrow(2); borrow(8);
various actions; various actions;
repay(10) repay(24)
If the bank has a cash reserve of $30 or more (the sum of their credit limits), Alice and Bob can perform these actions whenever they like and no problem will occur. But suppose the bank has a cash reserve of just $25. Can anything go wrong?
Indeed, yes! Suppose Alice is the first to arrives. She asks the bank officer for $8. The officer obliges since the cash reserve is $25. After Alice gets her loan, the cash reserve is now $17. Next, Bob arrives and requests $16. Again the officer obliges, leaving the cash reserve at $1. Now the bank is in trouble. If Alice arrives next to claim $2, she must be told to wait since the cash reserve is only $1. Similarly, if Bob arrives to claim $8, he must be told to wait since the cash reserve is only $1. But this is a deadlock. Both Alice and Bob are waiting for each other, but neither can proceed and repay enough that the bank can honor either waiting request.
What is the problem here? It lies in the policy of granting a loan request if the cash reserve is sufficient. This policy can put the system into an unsafe state. In the example, as soon as Alice has $8 and Bob $16, the cash reserve is smaller than either one's next future request. Thus that future request cannot be granted. When both eventually arrive to make their future requests, they will encounter the deadlock.
Therefore, the bank must use a more sophisticated policy. If Alice arrives to make a request, the bank officer must look into the future and ask: "If I grant her request, will she and every other person who has a loan outstanding be able to get their future requests?". This means that the officer must compare the cash reserve after granting Alice's latest request with the maximum future request every other borrower can make. (The maximum future request is the difference between the person's current outstanding loan and the line of credit.) If everyone's maximum future request cannot be met from the proposed cash reserve, the officer must tell Alice to wait. If at least one borrower's maximum future request can be met, the bank officer can grant Alice's request while remembering that the other borrower must be given priority for his future requests.
| The algorithms for keeping the system in safe states get rather complex and it is unattractive to use them. |
With this strategy the bank officer can tell if a proposed state would be unsafe, and he obtains a way to sequence the borrowers to guarantee that all resources will eventually be released. Does this seem to be complicated? It is. It gets even more so if there are many borrowers and they can deal in multiple currencies. The algorithms for keeping the system in safe states get rather complex and it is unattractive to use them. For this reason, many a system administrator prefers to allow the system to run; if ever it appears that some subset of it is stuck, the administrator runs a detection algorithm. If the detector finds a deadlock, the system administrator can abort the affected processes until enough resources have been freed to permit the others to continue.
Deadlock Detection
The usual method of detecting a deadlock is to construct a diagram showing processes and resources. Each process and each resource unit is depicted as a node. Resource nodes are annotated with the number of available units. Whenever a process holds units of resource, we draw an arrow from the resource to the process, labeled with the number of units held. Whenever a process requests units of a resources (and is waiting), we draw an arrow from the process to the resource, labeled with the number of units requested. This diagram represents a current system state. Whenever a process makes a new request or releases a resource unit, the state diagram is updated accordingly.
A circular wait corresponds to a closed path in this diagram. For example, the kitchen example in the deadlock state looks like:
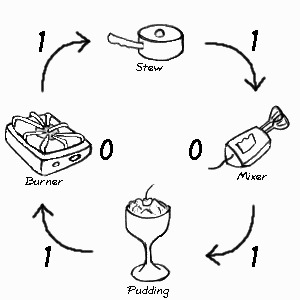
When there is just one unit of every resource, a circular wait in the diagram is equivalent to a deadlock in the system.
In the banking example, which has multiple units of each resource (its cash reserves in each currency), a loop in the diagram represents only a potential deadlock. Whether it is a real deadlock depends on whether any of the resources has fewer units available than any of the incoming request arrows:
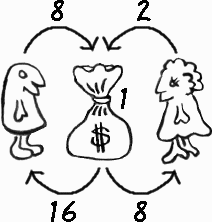
These examples show the principle of a deadlock detector: find all the loops in the current allocation diagram and see if any of them contains a resource that has too few units left to grant any of the incoming requests.
Conclusions
Deadlock is a system-wide phenomenon that can occur in any collection of processes that can stop and wait for resources held by other processes. In some cases, it can be prevented outright. Two strategies for doing this are (1) force a process to acquire all resources it needs before it begins, and (2) force a process to acquire new resources in a priority order.
In some cases, deadlock can be avoided even if neither of these strategies is usable. The central idea is that a system controller monitors each request for additional resource, granting it only if there is a way to run all the processes to completion and release that resource again. It's akin to the traffic rule that says don't enter an intersection unless there is room for you to exit it. This strategy is too expensive for many systems, especially those with many processes and many resources.
Deadlock detectors are easy to build, but cannot prevent the cost of having to abort some processes to free up the deadlock.
Which strategy is best for a given application depends on the requirements faced by the system designer. A critical real-time system, such as the control system on a space satellite, must be designed to be free of deadlock. It may otherwise be impossible to release the system from a deadlock state if one occurs. In other systems, such as a database with many transactions attempting to lock multiple records, an occasional deadlock can be tolerated if the results of a transaction are not committed into the database until after the transaction is finished.